Dans le cadre de mes recherches, j’ai eu besoin de générer des maillages depuis des pavages de Voronoï. Je mets donc à disposition de tout un chacun mon code C++ pour convertir des données Voro++ en fichier de géométrie pour Gmsh.
Table des matières
Introduction
Pavage de Voronoï
Le pavage de Voronoï consiste à séparer un espace $latex \Omega$ en $latex n$ cellules. Chaque cellule $latex i$ est définie par les coordonnées de son « site » $latex (X_i,Y_i)$ (je prends dans cet exemple $latex \Omega\subset\mathbb{R}^2$) de façon à ce que, en tout point de $latex \Omega$, la distance euclidienne de ce point par rapport au site associé soit minimale. En d’autre termes :
$latex \forall \boldsymbol{x}\in\Omega\quad i(\boldsymbol{x})=\mathrm{arg\,min}_k\left\lVert\boldsymbol{x}-\boldsymbol{x}_k\right\rVert$
où $latex i(\boldsymbol{x})$ est l’indice de la cellule en $latex \boldsymbol{x}$ et $latex \boldsymbol{x}_k$ les coordonnées du site $latex k$.

Pavage de Laguerre-Voronoï
La pavage de Laguerre-Voronoï (ou Voronoï radical) consiste à considérer qu’un site est caractérisé par un rayon, en plus de ses coordonnées. Si on note $latex r_k$ le rayon du site $latex k$, on a alors :
$latex \forall \boldsymbol{x}\in\Omega\quad i(\boldsymbol{x})=\mathrm{arg\,min}_k\left(\lVert\boldsymbol{x}-\boldsymbol{x}_k\rVert^2-r_k^2\right)$
L’avantage de ce pavage est donc que l’on peut (un peu) contrôler la taille des cellules grâce aux rayons des sites.
Voro++
Voro++ est une librairie C++ pour le pavage Voronoï et Laguerre-Voronoï. Il a été développé par Chris Rycroft pendant sa thèse au MIT.
Objectif de la classe proposée
La classe que j’ai développée (vorogmsh) permet d’extraire la géométrie obtenue après pavage de Laguerre-Voronoï sous Voro++ et de l’exporter en fichier texte, lisible par Gmsh. Ce dernier peut alors être utilisé pour mailler chaque cellule séparément (tout en ayant cohérence des nœuds aux frontières). Vous trouverez toutes les sources sur GitHub.
Voici une illustration du résultat obtenu :
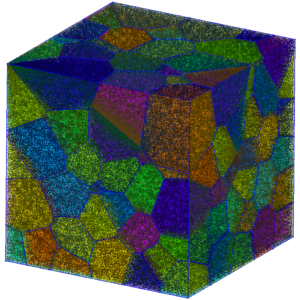
C’est pour cette classe que j’avais développé adjacencyMatrix, qui permet de manipuler facilement des matrices d’adjacence orientées.
Restrictions
Pour l’instant, le code proposé ne fonctionne qu’avec :
- le pavage de Laguerre-Voronoï
- pas de périodicité aux bords du domaine
Il est facile de réécrire le code pour palier le point 1 (il suffit de réécrire le constructeur pour un argument de type container à la place de container_poly, ou de créer un template). Mais n’en ayant pas d’utilité, je laisse le soin de le faire à qui s’en sentirait le besoin :-). Le point 2 est quant à lui beaucoup plus délicat, et pour l’instant je n’ai réussi à le résoudre…
De plus, il faut bien reconnaître que je suis à peu près aussi habile avec une guitare qu’avec un clavier devant Code : :Blocks, donc les puristes pleureront probablement du sang en voyant mon code ; mais au moins ça fait le job ! Donc toute contribution est la bienvenue.

