Si vous faites un peu de cristallographie ou avez souvent à représenter des ensembles d’orientations dans l’espace, alors vous devez connaître les figures de pôles.

Je vous donne ici une solution que j’ai développée pour tracer ces figures de pôles directement sous $latex \LaTeX$ grâce à la librairie polar de PGFPlots et la surpuissante option filter.

Exemple

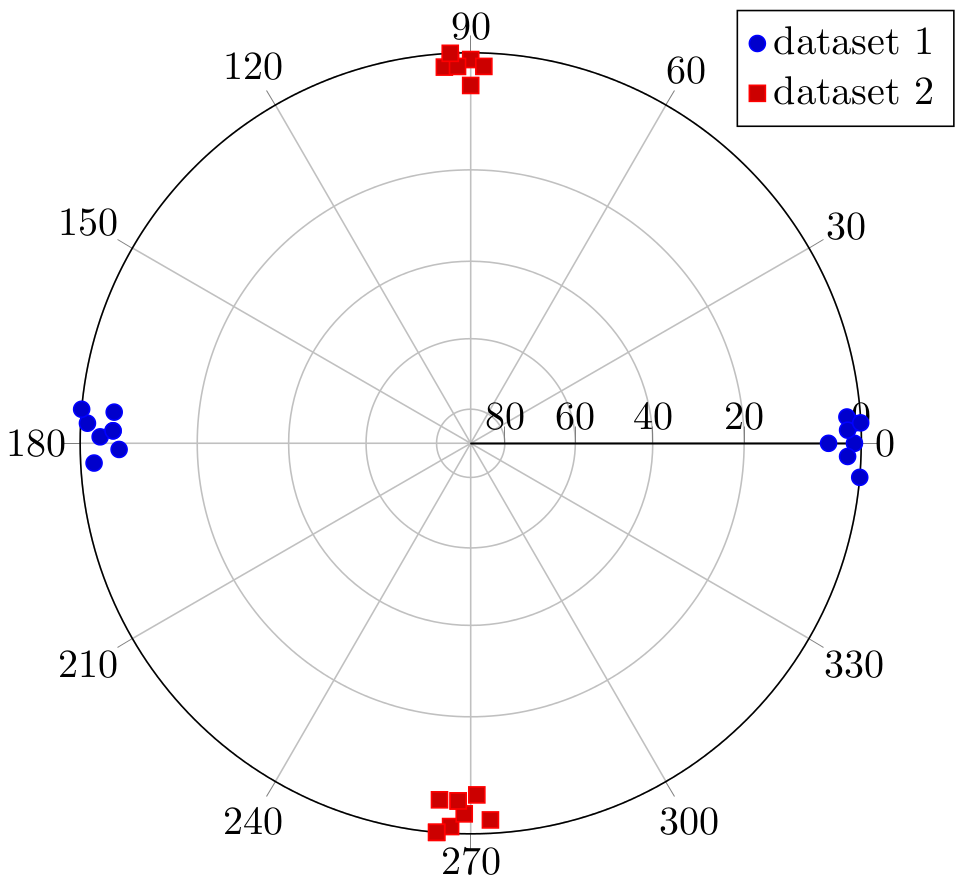
Code

Préambule

\usepackage{pgfplots}
	\pgfplotsset{compat=1.12}
\usepgfplotslibrary{polar}
 
 
% Courbes iso-theta
\newcommand{\thetaTicks}[1]{
	\gdef\listticks{}% global list
	\gdef\listticklabels{}
	\foreach \itheta[count=\xi] in {#1}{
		\global\let\maxitems\xi 			% Décompte de nombres de labels
	}
	\foreach \itheta[count=\xi] in {#1}{
		% \r = Rayon des iso dans le plan de projection
		\pgfmathparse{cos(\itheta)/(1+sin(\itheta)}\let\r\pgfmathresult
		\ifnum\xi=\maxitems
			\xdef\listticks{\listticks \r}
			\xdef\listticklabels{\listticklabels \itheta}
		\else
			\xdef\listticks{\listticks \r,}
			\xdef\listticklabels{\listticklabels \itheta,}
		\fi
	}
	\edef\setthetaticks{%
		% http://tex.stackexchange.com/questions/17833/using-macro-defined-lists-in-tikz-pgfplots
		\noexpand\pgfplotsset{%
			y tick labels list/.style={yticklabels={\listticklabels}}
		}%
	}	
}
 
\thetaTicks{0,20,...,80}	% Liste des iso-theta
 
 
\newenvironment{polefigure}[1][]{
	\setthetaticks
	\begin{polaraxis}[
		xmin=0,xmax=360,		% phi
		ymin=0,ymax=1,		% rayon
		ytick={\listticks},
		y tick labels list,
		#1, 					% Argument facultatif à la macro
		y filter/.code={
			% Projection stéréo
			\pgfmathparse{cos(\pgfmathresult)/(1+abs(sin(\pgfmathresult)))}
		}]
}{
	\end{polaraxis}
}

Corps de document

\begin{tikzpicture}
	\begin{polefigure}
		\addplot table[x=psi, y=theta]  {dataset1.csv};
	\end{polefigure}
\end{tikzpicture}

Comment ça marche ?

On utilise ici l’option filter, pour appliquer une transformation aux coordonnées : on passe des coordonnées $latex \phi,\theta$ aux coordonnées polaires $latex \theta,r(\theta)$ (voir le détail ci-dessous). L’avantage de cette méthode plutôt que d’exécuter des opérations à la volée (comme je le détaillais ici), c’est que la transformation se fait de façon totalement transparente. Ainsi, toutes les commandes habituelles restent inchangées (j’aurais tout aussi bien pu utiliser un \addplot coordinates{} par exemple).

Si vous voulez plus d’informations sur le filtrage des données, le mieux est de s’en référer au manuel de PGFPlots (pages 367 à 371).

Les maths

La projection de chaque point est ici faite dans le plan équateur ($latex z=0$) par rapport au pôle opposé, comme illustré ci après :

Dans le cas $latex z \geq0$, la projection se fait par rapport au pôle sud. On a donc :

$latex \overrightarrow{OP’_1}=\overrightarrow{OS}+\overrightarrow{SP’_1}$

Soit $latex (x_1,y_1,z_1)$ les coordonnées cartésiennes de $latex P_1$. On pose :

$latex \overrightarrow{SP’_1}=\lambda \overrightarrow{SP_1}$

Sachant que le point $latex M$ est compris dans le plan $latex z=0$, on trouve  :

$latex \lambda=\frac{1}{1+z_1}$.

De la même manière, on trouverait pour $latex z\leq 0$ :

$latex \lambda=\frac{1}{1-z_1}\,$

On peut donc généraliser :

$latex \lambda=\frac{1}{1+|z_1|}$.

Dans mon cas, chaque point de l’espace est caractérisé par ses coordonnées sphériques $latex (\phi,\theta)$, respectivement l’azimut (orientation dans le plan $latex x-y$) et la latitude $latex \theta$. On a donc :

$latex
\left\lbrace
\begin{aligned}
x_1 &=\cos\theta\cos\phi\\
y_1 &=\cos\theta\cos\phi\\
z_1 &=\sin\theta\\
\end{aligned}
\right.
$

Chaque projection est caractérisé par ses coordonnées polaires $latex (\phi,r)$. On a donc enfin :

$latex r=\frac{\cos\theta}{1+|\sin\theta|}$